皆さんは雨が降っている日に傘をさしているのに濡れたこんな経験はありませんか?僕は傘をさすのが下手なのかズボンがびしょ濡れになりました。
感覚的に傘の角度を調整していますが、最も濡れない角度を雨が降る角度によって考えてみたいと思います。
先に結論から話すと正しい角度は「向かってくる雨に傘を垂直な角度」です。当たり前のことなのですが、実際に具体的な速度で確認してみましょう。
考え方
降ってくる雨から体が最も濡れない角度は「自分から見た雨の進行方向に対して、傘の面が垂直になる角度」です。止まっているときに真上からの雨は、歩き出すと前方から斜めに降ってくるように見えます。この見かけの雨に対して傘が最も広い盾となるように構えるのが、最も効果的なのです。
物理的に言うと自身と雨の相対速度に対して自身の有効面積を最も小さくできる角度なのです。
これを様々な状況で考えてみましょう。
問題の設定
問題を3つの要因だけで考えて、
- 歩く速さ:v
- 雨の速度:u
- 傘の角度:θ
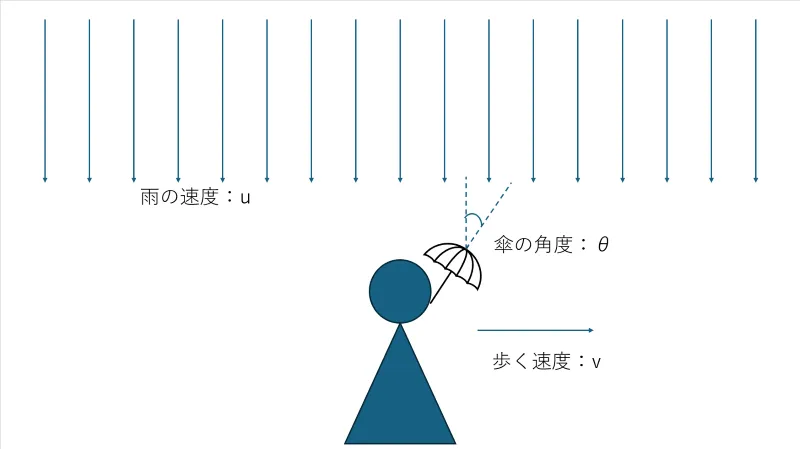
このような図の設定を考えます。
歩いているときに雨が真上から降り注ぐ場合は、斜め前から雨が降るように感じます。これは相対速度の影響であり、歩いている人から見た雨の速度(以降:相対速度)はu-vと考えられます。
(注意:uとvはベクトル量です。)
歩いている人の進行方向をx軸正の方向として、歩いている人の真上の方向をy軸正の方向とすると、u=(u1, u2)とv=(v1, v2)と表される。そのため、相対速度vrは
\vec{v}_{r} = \vec{u} - \vec{v} = (u_1, u_2) - (v_1, v_2) = (u_1-v_1,u_2- v_2)となります。この相対速度に対して傘を垂直に構えるのが最適なので、傘を傾けるべき角度θは、このベクトルがなす角度と同じになります。
図から、最適な角度 θ は以下の式で求められます。
\tan \theta = \frac{u_1-v_1}{u_2-v_2}よって、最適な傘の角度 θ は、
\theta = \arctan\left( \frac{u_1-v_1}{u_2-v_2}\right)と導出できます。
無風の時
この式に具体的な数値を入れて、実際の角度を考えてみる。
一般に歩く速さは約1.3m/sで表されることが多く、雨粒の終端速度は雨粒の大きさや形状によって異なりますが、今回は約6.5m/sとかていすると、これらの式は、u1=v2=0より、
\tan \theta =\frac{-v_1}{u_2}=\frac{-1.3\text{ m/s}}{-6.5\text{ m/s}}=\frac{1}{5}この tanθ の値から、角度 θ を求めます。
\theta = \arctan(\frac{1}{5}) \approx11.3^\circ計算の結果、約11° という角度が導き出されました。
これは傘を真上から進行方向にわずかに11.3°だけ傾けることで物理的に濡れなくなるのです。
風がある場合
風が吹いている場合は、さらに風の速度を考慮する必要があります。
今回はビューフォート風力階級で疾風である風速*¹を8.0m/sと仮定します。
(i)向かい風
向かい風の速さをwとすると、雨の見かけ上の水平速度はv1+wとなり
\tan \theta = \frac{-(v_1+w)}{u_2}=\frac{-(1.3+8.0)\text{ m/s}}{-6.5\text{ m/s}}=\frac{93}{65}ここから角度を求めると、
\theta = \arctan(\frac{93}{65}) \approx55.0^\circ無風のときと比べて、かなり大きく前方に傾ける必要がある。
(ii)追い風
追い風の場合は少し複雑で、雨の見かけ上の水平速度はv1-wとなるので
\tan \theta = \frac{-(v_1-w)}{u_2}=\frac{-(1.3-8.0)\text{ m/s}}{-6.5\text{ m/s}}=-\frac{67}{65}ここから角度を求めると、
\theta = \arctan(\frac{67}{65}) \approx-45.9^\circもし歩く速さより風が強い (w>v) なら、傘を後方に結構な角度傾ける必要がある。
余談
ちなみに風速が10m/sを超えると角度は60°になり、風速か歩く速さが速くなるにつれて傘を90°つまり、上にかざす必要がなくなります。
まとめ
実際の問題では、雨粒の形状や大きさや風の強さや加速度によって変わりますが、これからは雨が降った時、ただ傘をさすだけでなく、「今の自分の速度なら、角度は70°くらいかな?」と考えてみるのと面白いかもしれません!
ここまで読んでいただきありがとうございます。
ご意見・ご質問・ご要望がある方は以下のTwitterやInstagramのdmまでよろしくお願いいたします。
参照
*1:Beaufort scalehttps://en.wikipedia.org/wiki/Beaufort_scale



コメント